Περιεχόμενο
Ο νόμος των sines και ο νόμος των κοσκινών είναι τριγωνομετρικοί τύποι που αφορούν τα μέτρα των γωνιών ενός τριγώνου στα μήκη των πλευρών του. Προέρχονται από την ιδιότητα ότι οι μεγαλύτερες γωνίες στα τρίγωνα έχουν αναλογικά μεγαλύτερες απέναντι πλευρές. Χρησιμοποιήστε το νόμο των αιθουσών ή το νόμο των κοσκινών για να υπολογίσετε τα μήκη των πλευρών ενός τριγώνου και του τετράπλευρου (ένα τετράπλευρο είναι ουσιαστικά δύο γειτονικά τρίγωνα) εάν γνωρίζετε το μέτρο μιας πλευράς, μιας γωνίας και μιας επιπλέον πλευράς ή γωνίας.
Υπολογίστε τα τριγωνικά πλευρικά μήκη
Βρείτε τις δουλειές του τριγώνου. Τα δίδυμα είναι μήκη πλευρών και μέτρα γωνιών που είναι ήδη γνωστά.Δεν μπορείτε να βρείτε το μέτρο των τριγωνικών μακρών πλευρών εκτός αν γνωρίζετε το μέτρο μιας γωνίας, μιας πλευράς και μιας άλλης πλευράς ή άλλης γωνίας.
Χρησιμοποιήστε τα δεδομένα για να προσδιορίσετε αν το τρίγωνο είναι ένα τρίγωνο ASA, AAS, SAS ή ASS. Ένα τρίγωνο ASA έχει δύο γωνίες ως δίδυμα καθώς και την πλευρά που συνδέει τις δύο γωνίες. Ένα τρίγωνο AAS έχει δύο γωνίες και μια διαφορετική πλευρά ως δίδυμα. Ένα τρίγωνο SAS έχει δύο πλευρές ως δίδυμα καθώς και τη γωνία που σχηματίζεται από τις δύο πλευρές. Ένα τρίγωνο ASS έχει δύο πλευρές και μια διαφορετική γωνία όπως οι δίδυμες.
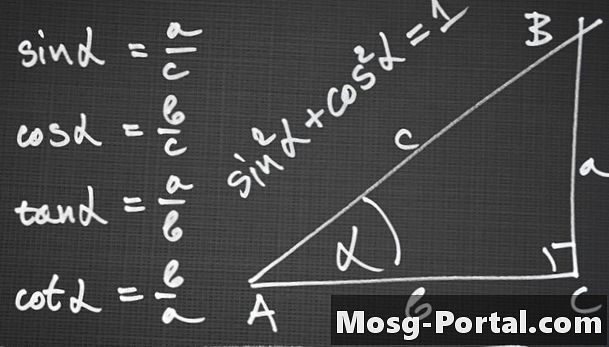
Χρησιμοποιήστε το νόμο του sines για να δημιουργήσετε μια εξίσωση σχετικά με τα μήκη των πλευρών αν είναι ένα τρίγωνο ASA, AAS ή ASS. Ο νόμος των sines δηλώνει ότι οι αναλογίες των sines των γωνιών των τριγώνων και των αντίθετων πλευρών τους είναι ίσες: sin a / a = sin B / b = αμαρτία C / c, όπου a, b και c είναι τα αντίθετα πλάτη των γωνιών Α, Β και Γ αντίστοιχα.
Για παράδειγμα, εάν γνωρίζετε ότι οι δύο γωνίες είναι 40 μοίρες και 60 μοίρες και η πλευρά που ενώνει τους έχει μήκος 3 μονάδων, θα στήσετε την εξίσωση sin 80/3 = sin 40 / b = sin 60 / c η πλευρά που έχει μήκος 3 μονάδων είναι 80 μοίρες επειδή το άθροισμα των γωνιών των τριγώνων είναι 180 μοίρες).
Χρησιμοποιήστε το νόμο των κοσκινών για να δημιουργήσετε μια εξίσωση σχετικά με τα μήκη των πλευρών αν είναι ένα τρίγωνο SAS. Ο νόμος των κοσκινών δηλώνει ότι το c 2 = a ^ 2 + b ^ 2 - 2ab_cos C. Με άλλα λόγια, το τετράγωνο του μήκους της πλευράς c είναι ίσο με τα τετράγωνα των άλλων δύο πλευρών μείον το προϊόν αυτών των δύο τις πλευρές και το συνημίτονο της γωνίας απέναντι από την άγνωστη πλευρά. Για παράδειγμα, εάν οι δύο πλευρές ήταν 3 μονάδες και 4 μονάδες και η γωνία ήταν 60 μοίρες, θα γράφετε την εξίσωση c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4 * cos 60.
Λύστε τις μεταβλητές στις εξισώσεις για να βρείτε τα άγνωστα μήκη τρίγωνου. Η επίλυση για το b στην εξίσωση sin 80/3 = sin 40 / b αποδίδει την τιμή b = 3 sin 40 / sin 80, οπότε το b είναι περίπου 2. Η επίλυση για c στην εξίσωση sin 80/3 = sin 60 / c τιμή c = 3 sin 60 / sin 80, έτσι ώστε το c να είναι περίπου 2.6. Ομοίως, η επίλυση για το c στην εξίσωση c ^ 2 = 3 ^ 2 + 4 ^ 2-3_4_cos 60 αποδίδει την τιμή c ^ 2 = 25-6 ή c ^ 2 = 19, έτσι c είναι περίπου 4.4.
Υπολογίστε τα τετράπλευρα μήκη πλευρών
Σχεδιάστε μια διαγώνιο μέσα από το τετράπλευρο (επιλέξτε τη διαγώνιο που δεν περιλαμβάνει οποιαδήποτε δεδομένη γωνία, για παράδειγμα, αν η γωνία Α είναι δεδομένη στην τετράπλευρη ABCD, τραβήξτε τη διαγώνιο που συνδέει τα B και D).
Χρησιμοποιήστε τα δεδομένα για να δημιουργήσετε ένα τρίγωνο ASA, SAS, AAS ή ASS. Θυμηθείτε ότι το άθροισμα των γωνιών ενός τετράπλευρου είναι 360 μοίρες, έτσι μπορείτε να βρείτε το μέτρο της τέταρτης γωνίας αν γνωρίζετε τα άλλα τρία.
Χρησιμοποιήστε το νόμο του sines για να λύσετε τα μήκη των πλευρών του τετράπλευρου εάν δημιουργήσετε ένα τρίγωνο ASA, AAS ή ASS. Χρησιμοποιήστε το νόμο των κοσκινών για να λύσετε τα μήκη των πλευρών αν έχετε δημιουργήσει ένα τρίγωνο SAS.