Περιεχόμενο
- TL · DR (Πολύ μακρύ;
- Φόρμουλα για ταχύτητα
- Τύπος ταχύτητας
- Εξίσωση για επιτάχυνση
- Ηλεκτρονικοί υπολογιστές
- Προειδοποιήσεις
Τα προβλήματα που αφορούν τον υπολογισμό της ταχύτητας, της ταχύτητας και της επιτάχυνσης εμφανίζονται συνήθως στη φυσική. Συχνά αυτά τα προβλήματα απαιτούν τον υπολογισμό των σχετικών κινήσεων των τρένων, των αεροπλάνων και των αυτοκινήτων. Αυτές οι εξισώσεις μπορούν επίσης να εφαρμοστούν σε πιο σύνθετα προβλήματα όπως η ταχύτητα του ήχου και του φωτός, η ταχύτητα των πλανητικών αντικειμένων και η επιτάχυνση των ρουκετών.
TL · DR (Πολύ μακρύ;
Οι εξισώσεις για την ταχύτητα, την ταχύτητα και την επιτάχυνση εξαρτώνται από τη μεταβολή της θέσης με την πάροδο του χρόνου. Η μέση ταχύτητα χρησιμοποιεί την εξίσωση "η ταχύτητα ισούται με τη διανυθείσα απόσταση (d) διαιρούμενη με το χρόνο διαδρομής (t)," ή τη μέση ταχύτητα = d ÷ t. Η μέση ταχύτητα ισούται με την ταχύτητα σε μια κατεύθυνση. Η μέση επιτάχυνση (α) ισούται με τη μεταβολή της ταχύτητας (Δv) που διαιρείται με το χρονικό διάστημα της μεταβολής της ταχύτητας (Δt), ή a = Δv ÷ Δt.
Φόρμουλα για ταχύτητα
Η ταχύτητα αναφέρεται στην απόσταση που διανύθηκε κατά τη διάρκεια μιας χρονικής περιόδου. Ο συνήθης τύπος για την ταχύτητα υπολογίζει τη μέση ταχύτητα παρά την στιγμιαία ταχύτητα. Ο υπολογισμός μέσης ταχύτητας δείχνει τη μέση ταχύτητα ολόκληρου του ταξιδιού, αλλά η στιγμιαία ταχύτητα δείχνει την ταχύτητα σε οποιαδήποτε δεδομένη στιγμή του ταξιδιού. Ένα ταχύμετρο οχημάτων δείχνει στιγμιαία ταχύτητα.
Η μέση ταχύτητα μπορεί να βρεθεί χρησιμοποιώντας τη συνολική απόσταση που διανύθηκε, συνήθως συντομευμένη ως d, διαιρούμενη με το συνολικό χρόνο που απαιτείται για τη διαδρομή αυτής της απόστασης, συνήθως συντομογραφία ως t. Έτσι, εάν ένα αυτοκίνητο διαρκεί 3 ώρες για να ταξιδέψει σε απόσταση 150 μιλίων, η μέση ταχύτητα ισούται με 150 μίλια διαιρούμενη με 3 ώρες, ισούται με μια μέση ταχύτητα 50 μίλια ανά ώρα (150 ÷ 3 = 50).
Η στιγμιαία ταχύτητα είναι ένας υπολογισμός ταχύτητας που θα συζητηθεί στο τμήμα ταχύτητας.
Μονάδες μήκους ή ταχύτητας εμφάνισης ταχύτητας με την πάροδο του χρόνου. Τα χιλιόμετρα ανά ώρα (mph / mph), τα χιλιόμετρα ανά ώρα (km / h ή kph), τα πόδια ανά δευτερόλεπτο (ft / s ή ft / sec) και τα μέτρα ανά δευτερόλεπτο (m / s).
Τύπος ταχύτητας
Η ταχύτητα είναι μια τιμή διανύσματος, που σημαίνει ότι η ταχύτητα περιλαμβάνει την κατεύθυνση. Η ταχύτητα ισούται με την διανυθείσα απόσταση διαιρούμενη με το χρόνο της διαδρομής (ταχύτητα) συν την κατεύθυνση της διαδρομής. Για παράδειγμα, η ταχύτητα ενός τρένου που ταξιδεύει 1.500 χιλιόμετρα ανατολικά από το Σαν Φρανσίσκο σε 12 ώρες θα είναι 1.500 χιλιόμετρα διαιρούμενο με 12 ώρες ανατολικά, ή 125 χιλιόμετρα ανατολικά.
Επιστρέφοντας στο πρόβλημα της ταχύτητας των αυτοκινήτων, εξετάστε δύο αυτοκίνητα που ξεκινούν από το ίδιο σημείο και ταξιδεύουν με την ίδια μέση ταχύτητα 50 μίλια ανά ώρα. Εάν ένα αυτοκίνητο ταξιδεύει βόρεια και το άλλο αυτοκίνητο ταξιδεύει δυτικά, τα αυτοκίνητα δεν καταλήγουν στην ίδια θέση. Η ταχύτητα του βόρειου αυτοκινήτου θα είναι 50 mph βόρεια και η ταχύτητα του δυτικού αυτοκινήτου θα είναι 50 mph δυτικά. Οι ταχύτητές τους είναι διαφορετικές, παρότι οι ταχύτητές τους είναι ίδιες.
Η στιγμιαία ταχύτητα, για να είναι απόλυτα ακριβής, απαιτεί να υπολογιστεί ο υπολογισμός, διότι η προσέγγιση "στιγμιαίας" απαιτεί μείωση του χρόνου στο μηδέν. Ωστόσο, μπορεί να γίνει προσέγγιση με τη χρήση της στιγμιαίας ταχύτητας εξίσωσης (vΕγώ) ισούται με τη μεταβολή της απόστασης (Δd) διαιρούμενη με την αλλαγή του χρόνου (Δt), ή vΕγώ = Δd ÷ Δt. Με τον καθορισμό της αλλαγής του χρόνου ως πολύ σύντομο χρονικό διάστημα, μπορεί να υπολογιστεί μια σχεδόν στιγμιαία ταχύτητα. Το ελληνικό σύμβολο για το δέλτα, ένα τρίγωνο (Δ), σημαίνει αλλαγή.
Για παράδειγμα, εάν ένα κινούμενο τρένο έχει ταξιδέψει 55 χλμ. Ανατολικά στις 5:00 και έχει φτάσει στα 65 χλμ. Ανατολικά στις 6:00, η αλλαγή στην απόσταση είναι 10 χλμ. Ανατολικά με αλλαγή ώρας ως 1 ώρα. Εισαγωγή αυτών των τιμών στον τύπο vΕγώ = Δv ÷ Δt δίνει vΕγώ = 10 ÷ 1, ή 10 kph ανατολικά (βεβαίως μια αργή ταχύτητα για ένα τρένο). Η στιγμιαία ταχύτητα θα ήταν 10 χιλιόμετρα ανατολικά, διαβάστηκε στο ταχύμετρο των κινητήρων ως 10 χιλιόμετρα / ώρα. Φυσικά, μια ώρα δεν είναι "στιγμιαία", αλλά χρησιμεύει ως παράδειγμα.
Ας υποθέσουμε ότι ένας επιστήμονας μετρά την αλλαγή θέσης (Δd) ενός αντικειμένου ως 8 μέτρα σε χρονικό διάστημα (Δt) 2 δευτερολέπτων. Χρησιμοποιώντας τον τύπο, η στιγμιαία ταχύτητα ισούται με 4 μέτρα ανά δευτερόλεπτο (m / s) με βάση τον υπολογισμό vΕγώ = Δd ÷ Δt ή vΕγώ = 8 ÷ 2 = 4.
Ως ποσότητα φορέα, η στιγμιαία ταχύτητα πρέπει να περιλαμβάνει κατεύθυνση. Πολλά προβλήματα, ωστόσο, υποθέτουν ότι το αντικείμενο συνεχίζει να ταξιδεύει προς την ίδια κατεύθυνση κατά τη διάρκεια αυτού του σύντομου χρονικού διαστήματος. Στη συνέχεια αγνοείται η κατεύθυνση του αντικειμένου, γεγονός που εξηγεί γιατί αυτή η τιμή ονομάζεται συχνά στιγμιαία ταχύτητα.
Εξίσωση για επιτάχυνση
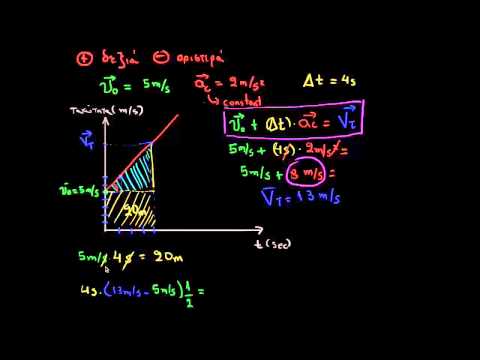
Ποιος είναι ο τύπος για την επιτάχυνση; Η έρευνα δείχνει δύο προφανώς διαφορετικές εξισώσεις. Μια φόρμουλα, από τον δεύτερο νόμο του Νεύτων, αναφέρεται στη δύναμη, τη μάζα και την επιτάχυνση στη δύναμη εξίσωσης (F) ισούται με την επιτάχυνση μάζας (m) φορές (a), γραμμένη ως F = ma. Ένας άλλος τύπος, η επιτάχυνση (α) ισούται με τη μεταβολή της ταχύτητας (Δv) διαιρούμενη με την αλλαγή του χρόνου (Δt), υπολογίζει το ρυθμό μεταβολής της ταχύτητας με την πάροδο του χρόνου. Ο τύπος αυτός μπορεί να γραφεί a = Δv ÷ Δt. Δεδομένου ότι η ταχύτητα περιλαμβάνει τόσο την ταχύτητα όσο και την κατεύθυνση, οι μεταβολές στην επιτάχυνση μπορεί να προκύψουν από αλλαγές στην ταχύτητα ή την κατεύθυνση ή και από τις δύο. Στην επιστήμη, οι μονάδες επιτάχυνσης συνήθως θα είναι μέτρα ανά δευτερόλεπτο ανά δευτερόλεπτο (m / s / s) ή μέτρα ανά δευτερόλεπτο σε τετράγωνο (m / s2).
Αυτές οι δύο εξισώσεις, F = ma και a = Δv ÷ Δt, δεν είναι σε αντίθεση μεταξύ τους. Το πρώτο δείχνει τη σχέση δύναμης, μάζας και επιτάχυνσης. Η δεύτερη υπολογίζει την επιτάχυνση με βάση την μεταβολή της ταχύτητας σε μια χρονική περίοδο.
Οι επιστήμονες και οι μηχανικοί αναφέρονται στην αυξανόμενη ταχύτητα ως θετική επιτάχυνση και μειούμενη ταχύτητα ως αρνητική επιτάχυνση. Οι περισσότεροι άνθρωποι, ωστόσο, χρησιμοποιούν τον όρο επιβράδυνση αντί για αρνητική επιτάχυνση.
Ενταση βαρύτητος
Κοντά στην επιφάνεια της Γης, η επιτάχυνση της βαρύτητας είναι σταθερή: a = -9,8 m / s2 (μέτρα ανά δευτερόλεπτο ανά δευτερόλεπτο ή μέτρα ανά δευτερόλεπτο τετράγωνο). Όπως πρότεινε το Galileo, αντικείμενα με διαφορετικές μάζες βιώνουν την ίδια επιτάχυνση από τη βαρύτητα και θα πέσουν με την ίδια ταχύτητα.
Ηλεκτρονικοί υπολογιστές
Με την εισαγωγή δεδομένων σε έναν ηλεκτρονικό υπολογισμό ταχύτητας, μπορεί να υπολογιστεί η επιτάχυνση. Οι ηλεκτρονικοί υπολογιστές μπορούν να χρησιμοποιηθούν για τον υπολογισμό της εξίσωσης ταχύτητας με την επιτάχυνση και τη δύναμη. Η χρήση αριθμομηχανής επιτάχυνσης και απόστασης απαιτεί γνώση της ταχύτητας και του χρόνου.