Περιεχόμενο
- Μέτρα μεταβλητότητας
- Διακύμανση Φόρμουλα
- Τυπική απόκλιση
- Απόκλιση δείγματος και πρόβλημα τυπικής απόκλισης
Η ικανότητα να υπολογίζεται η μέση ή μέση τιμή μιας ομάδας αριθμών είναι σημαντική σε κάθε πτυχή της ζωής. Εάν είστε καθηγητής που ορίζει βαθμολογίες επιστολών σε βαθμολογίες εξετάσεων και παραδοσιακά δίνουν ένα βαθμό Β- σε μια βαθμολογία μεσαίας κλίμακας, τότε σαφώς πρέπει να ξέρετε τι μοιάζει με τη μέση της συσκευασίας. Χρειάζεστε επίσης έναν τρόπο να προσδιορίσετε τις βαθμολογίες ως υπερβάσεις, ώστε να μπορείτε να προσδιορίσετε πότε κάποιος αξίζει έναν Α ή Α + (εκτός από τέλειες βαθμολογίες, προφανώς) καθώς και τι αξίζει ένα βαθμίδα που αποτυγχάνει.
Για αυτό και τους συναφείς λόγους, τα πλήρη στοιχεία σχετικά με τους μέσους όρους περιλαμβάνουν πληροφορίες σχετικά με το πόσο συγκεντρωμένα γύρω από το μέσο σκορ τα αποτελέσματα είναι γενικά. Αυτές οι πληροφορίες μεταφέρονται χρησιμοποιώντας τυπική απόκλιση και, συναφώς, το διαφορά ενός στατιστικού δείγματος.
Μέτρα μεταβλητότητας
Έχετε σχεδόν ακούσει ή έχετε δει τον όρο "μέσος όρος" που χρησιμοποιείται σε σχέση με ένα σύνολο αριθμών ή σημείων δεδομένων και ίσως έχετε μια ιδέα για το τι μεταφράζεται στην καθημερινή γλώσσα. Για παράδειγμα, αν διαβάσετε ότι το μέσο ύψος μιας αμερικανικής γυναίκας είναι περίπου 5 4 ", καταλήγετε αμέσως στο συμπέρασμα ότι" ο μέσος όρος "σημαίνει" τυπικός "και ότι περίπου οι μισές γυναίκες στις Ηνωμένες Πολιτείες είναι ψηλότερες από αυτό, ενώ περίπου το μισό είναι μικρότερες.
Μαθηματικά, ο μέσος όρος και ο μέσος είναι ακριβώς το ίδιο πράγμα: Προσθέτετε τις τιμές σε ένα σετ και διαιρείτε με τον αριθμό των αντικειμένων στο σετ. Για παράδειγμα, αν μια ομάδα 25 βαθμολογήσει σε μια κλίμακα δοκιμών 10 ερωτήσεων από 3 έως 10 και προσθέσει έως και 196, η μέση (μέση) βαθμολογία είναι 196/25 ή 7.84.
Ο διάμεσος είναι η τιμή του μεσαίου σημείου σε ένα σετ, ο αριθμός ότι οι μισές από τις τιμές βρίσκονται πάνω και οι μισές από τις τιμές βρίσκονται κάτω. Είναι συνήθως κοντά στον μέσο όρο, αλλά δεν είναι το ίδιο πράγμα.
Διακύμανση Φόρμουλα
Αν βγάλετε ένα σύνολο 25 βαθμών όπως τα παραπάνω και δεν βλέπετε σχεδόν τίποτα από τις τιμές των 7, 8 και 9, κάνει διαισθητική νόημα ότι ο μέσος όρος θα πρέπει να είναι περίπου 8. Αλλά τι εάν δεν βλέπετε σχεδόν τίποτα από τα αποτελέσματα των 6 και 10 ; Ή πέντε αποτελέσματα 0 και 20 σκορ 9 ή 10; Όλα αυτά μπορούν να παράγουν τον ίδιο μέσο όρο.
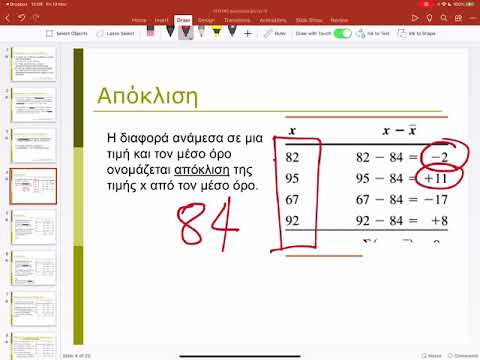
Η απόκλιση είναι ένα μέτρο του βαθμού εξάπλωσης των σημείων σε ένα σύνολο δεδομένων σχετικά με τον μέσο όρο. Για να υπολογίσετε τη διακύμανση με το χέρι, λαμβάνετε την αριθμητική διαφορά μεταξύ καθενός από τα σημεία δεδομένων και τον μέσο όρο, τετραγωνίζετε τα, προσθέτετε το άθροισμα των τετραγώνων και διαιρείτε το αποτέλεσμα κατά ένα μικρότερο από τον αριθμό των σημείων δεδομένων στο δείγμα. Ένα παράδειγμα αυτού παρέχεται αργότερα. Μπορείτε επίσης να χρησιμοποιήσετε προγράμματα όπως το Excel ή ιστοσελίδες όπως οι Ταχείες Πινάκες (δείτε τους πόρους για πρόσθετους ιστότοπους).
Η διακύμανση υποδηλώνεται από το σ2, ελληνικό "σίγμα" με εκθέτη 2.
Τυπική απόκλιση
Η τυπική απόκλιση ενός δείγματος είναι απλά η τετραγωνική ρίζα της διακύμανσης. Τα τετράγωνα λόγων χρησιμοποιούνται όταν υπολογίζεται η διακύμανση είναι ότι αν προσθέσετε απλώς μαζί τις μεμονωμένες διαφορές μεταξύ του μέσου και κάθε μεμονωμένου σημείου δεδομένων, το άθροισμα είναι πάντα μηδενικό επειδή ορισμένες από αυτές τις διαφορές είναι θετικές και μερικές είναι αρνητικές και ακυρώνονται η μία την άλλη . Η κατάκτηση κάθε όρου εξαλείφει αυτή την παγίδα.
Απόκλιση δείγματος και πρόβλημα τυπικής απόκλισης
Υποθέστε ότι έχετε δώσει τα 10 σημεία δεδομένων:
4, 7, 10, 5, 7, 6, 9, 8, 5, 9
Βρείτε τον μέσο όρο, τη διακύμανση και την τυπική απόκλιση.
Αρχικά, προσθέστε τις 10 τιμές μαζί και διαιρέστε με 10 για να πάρετε τον μέσο (μέσο):
70/10 = 7.0
Για να λάβετε τη διακύμανση, τετραγωνίζετε τη διαφορά μεταξύ κάθε σημείου δεδομένων και του μέσου όρου, προσθέστε τα μαζί και διαιρέστε το αποτέλεσμα με (10 - 1) ή 9:
9 + 0 + 9 + . . . + 4 = 36
σ2= 36/9 = 4.0
Η τυπική απόκλιση σ είναι μόνο η τετραγωνική ρίζα του 4.0 ή 2.0.