Μια έλλειψη μπορεί να οριστεί σε επίπεδη γεωμετρία ως το σύνολο των σημείων έτσι ώστε το άθροισμα των αποστάσεων τους σε δύο σημεία (εστίες) να είναι σταθερό. Το προκύπτον σχήμα μπορεί επίσης να περιγραφεί μη μαθηματικά ως οβάλ ή "πεπλατυσμένος κύκλος". Οι ελλείψεις έχουν πολλές εφαρμογές στη φυσική και είναι ιδιαίτερα χρήσιμες στην περιγραφή των πλανητικών τροχιών. Η εκκεντρότητα είναι ένα από τα χαρακτηριστικά και η έλλειψη και είναι ένα μέτρο του πώς είναι κυκλική η έλλειψη.
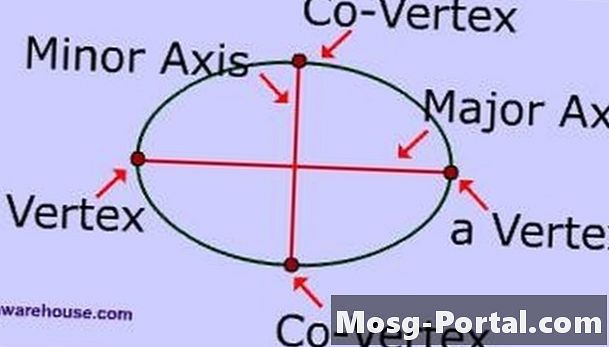
Εξετάστε τα τμήματα μιας έλλειψης. Ο κύριος άξονας είναι το μακρύτερο τμήμα γραμμής που τέμνει το κέντρο της ελλείψεως και έχει τα τελικά σημεία της ελλείψεως. Ο δευτερεύων άξονας είναι το μικρότερο τμήμα γραμμής που τέμνει το κέντρο της ελλείψεως και έχει τα τελικά σημεία της ελλείψεως. Ο κύριος ημι-άξονας είναι ο μισός από τον κύριο άξονα και ο μικρός ημι-άξονας είναι ο μισός άξονας.
Εξετάστε τον τύπο για έλλειψη. Υπάρχουν πολλοί διαφορετικοί τρόποι περιγραφής της έλλειψης μαθηματικά, αλλά η πιο χρήσιμη για τον υπολογισμό της εκκεντρότητάς της είναι η ελλειψία: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Οι σταθερές α και b είναι ειδικές για μια συγκεκριμένη έλλειψη και οι μεταβλητές είναι οι συντεταγμένες x και y των σημείων που βρίσκονται στην έλλειψη. Αυτή η εξίσωση περιγράφει μια έλλειψη με το κέντρο της στην αρχή και τους κύριους και δευτερεύοντες άξονες που βρίσκονται στις x και y καταγωγές.
Προσδιορίστε τα μήκη των ημι-αξόνων. Στην εξίσωση x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1, τα μήκη των ημιξονίων δίδονται από τα a και b. Η μεγαλύτερη τιμή αντιπροσωπεύει τον κύριο ημι-άξονα και η μικρότερη τιμή αντιπροσωπεύει τον μικρό ημι-άξονα.
Υπολογίστε τις θέσεις των εστιών. Οι εστίες βρίσκονται στον κύριο άξονα, ένα σε κάθε πλευρά του κέντρου. Δεδομένου ότι οι άξονες μιας έλλειψης βρίσκονται στις γραμμές προέλευσης, μία συντεταγμένη θα είναι 0 και για τις δύο εστίες. Η άλλη συντεταγμένη θα είναι (a ^ 2 - b ^ 2) ^ (1/2) για μία εστία και - (a ^ 2 - b ^ 2 ^ ^ 1/2 για τις άλλες εστίες όπου a> b.
Υπολογίστε την εκκεντρότητα της έλλειψης ως αναλογία της απόστασης μιας εστίας από το κέντρο προς το μήκος του ημι-κύριου άξονα. Επομένως η εκκεντρότητα e είναι (a ^ 2 - b ^ 2) ^ (1/2) / a. Σημειώστε ότι 0 <= e <1 για όλες τις ελλείψεις. Μια εκκεντρότητα 0 σημαίνει ότι η ελλειψοειδής είναι ένας κύκλος και μια μακρά, λεπτή έλλειψη έχει μια εκκεντρότητα που προσεγγίζει το 1.