Περιεχόμενο
Στη γεωμετρία, ένα οκτάγωνο είναι ένα πολύγωνο με οκτώ πλευρές. Ένα κανονικό οκτάγωνο έχει οκτώ ίσες πλευρές και ίσες γωνίες. Το κανονικό οκτάγωνο αναγνωρίζεται συνήθως από τα σήματα στάσης. Ένα οκτάεδρο είναι ένα πολυεδρικό οκτώ όψεων. Ένα κανονικό οκτάεδδρο έχει οκτώ τρίγωνα με άκρα ίσου μήκους. Είναι ουσιαστικά δύο τετράγωνα πυραμίδες που συναντώνται στις βάσεις τους.
Οκταγωνικός χώρος
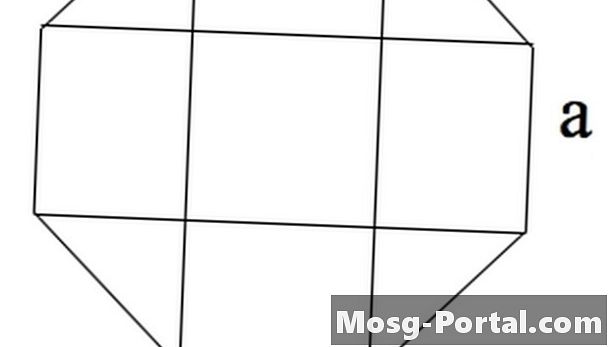
Ο τύπος για την περιοχή ενός κανονικού οκταγώνου με πλευρές μήκους "a" είναι 2 (1 + sqrt (2)) a ^ 2, όπου "sqrt" δηλώνει την τετραγωνική ρίζα.
Παραγωγή
Ένα οκτάγωνο μπορεί να θεωρηθεί ως 4 ορθογώνια, ένα τετράγωνο στο κέντρο και τέσσερα ισόγεια τρίγωνα στις γωνίες.
Το τετράγωνο είναι της περιοχής a ^ 2.
Τα τρίγωνα έχουν πλευρές a, a / sqrt (2) και a / sqrt (2), από το Πυθαγόρειο θεώρημα. Επομένως, το καθένα έχει μια περιοχή ^ 2/4.
Τα ορθογώνια είναι της περιοχής a * a / sqrt (2).
Το άθροισμα αυτών των 9 περιοχών είναι 2α ^ 2 (1 + sqrt (2)).
Τύπος όγκου Octahedron
Ο τύπος για τον όγκο ενός κανονικού οκτάεδρου των πλευρών «α» είναι ^ 3 * sqrt (2) / 3.
Παραγωγή
Η περιοχή μιας τετράπλευρης πυραμίδας είναι περιοχή βάσης * ύψος / 3. Η περιοχή ενός κανονικού οκταγώνου είναι επομένως 2 * βάση * ύψος / 3.
Βάση = a ^ 2 trivially.
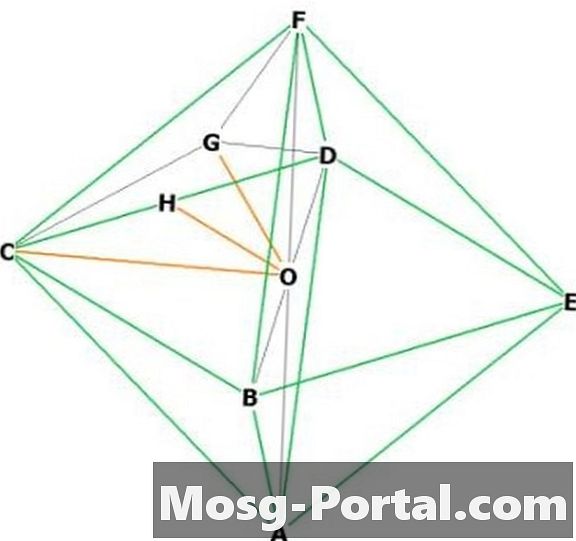
Επιλέξτε δύο γειτονικές κορυφές, π.χ. "F" και "C." Το "O" βρίσκεται στο επίκεντρο. Το FOC είναι ένα ορθογώνιο ορθογώνιο τρίγωνο με βάση "a", έτσι OC και OF έχουν μήκος a / sqrt (2) από το Πυθαγόρειο θεώρημα. Έτσι το ύψος = a / sqrt (2).
Έτσι, ο όγκος ενός κανονικού οκτάεδρου είναι 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Επιφάνεια
Η κανονική επιφάνεια των οκταεδρών είναι η περιοχή ενός ισόπλευρου τριγώνου πλευρικών "a" φορές 8 προσώπων.
Για να χρησιμοποιήσετε το θεώρημα Pythagorean, ρίξτε μια γραμμή από την κορυφή στη βάση. Αυτό δημιουργεί δύο ορθά τρίγωνα, με την υποτείνουσα μήκους "α" και μίας πλευράς μήκους "a / 2". Επομένως, η τρίτη πλευρά πρέπει να είναι sqrt = sqrt (3) a / 2. Έτσι η περιοχή ενός ισόπλευρου τριγώνου είναι ύψος * βάση / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Με 8 πλευρές, η επιφάνεια ενός κανονικού οκτάεδρου είναι 2 * sqrt (3) * a ^ 2.